Games are fun! Their well-defined rules let you explore different strategies in search of a surefire way to win. The minimax algorithm is used to choose the optimal move at any point in a game. You’ll learn how to implement a minimax player in Python that can play the game of Nim perfectly.
In this tutorial, you’ll focus on minimax. However, to visualize how the algorithm works, it’s nice to work with a concrete game. You’ll learn the rules of Nim, which is a game with simple rules and limited choices. Using Nim in the examples allows you to focus on the principles of minimax without getting lost in game rules.
As you follow this tutorial, you’ll:
- Learn the principles of the minimax algorithm
- Play several variants of the game of Nim
- Implement the minimax algorithm
- Lose Nim against a minimax player
- Use alpha-beta pruning to optimize the minimax algorithm
You can download the source code used in this tutorial, as well as a game simulator where you can play different variants of Nim against a minimax opponent, by clicking the link below:
Source Code: Click here to download the free source code that you’ll use to lose the game of Nim against your minimax player.
Play a Simplified Game of Nim
The roots of Nim go back a long time. While variants of the game have been played throughout history, Nim got its name in 1901 when Charles L. Bouton published Nim, a Game With a Complete Mathematical Theory.
Nim is a game for two players, which always ends with one player winning. The game consists of several counters lying on the game table and the players taking turns removing one or more counters. In the first half of this tutorial, you’ll play a simplified version of Nim with the following rules:
- There are several counters in a shared pile.
- Two players take alternating turns.
- On their turn, a player removes one, two, or three counters from the pile.
- The player that takes the last counter loses the game.
You’ll refer to this game as Simple-Nim. Later, you’ll learn the rules of regular Nim. They’re not much more complicated, but Simple-Nim is easier to reason about.
Note: Now it’s time to play! You’re going to start with the analog version, so clear a space on your desk. Play a few rounds of Simple-Nim to get a feel for the rules. Along the way, keep an eye out for any winning strategy that you come across.
You can use any objects that you happen to have available as counters, or you can use a notepad to keep track of the current number of counters in play. Somewhere between ten and twenty counters is a good starting point for a game.
If you don’t have an opponent nearby, you can play against yourself for now. By the end of the tutorial, you’ll have programmed an opponent that you can play against.
To demonstrate the rules, two players—Mindy and Maximillian—will play a game of Simple-Nim, starting with twelve counters. Mindy goes first:
- Mindy takes two counters, leaving ten in the pile.
- Maximillian takes one counter, leaving nine in the pile.
- Mindy takes three counters, leaving six in the pile.
- Maximillian takes two counters, leaving four in the pile.
- Mindy takes three counters, leaving one in the pile.
- Maximillian takes the last counter and loses the game.
In this game, Maximillian takes the last counter, so Mindy is the winner.
Nim, including Simple-Nim, is an intriguing game because the rules are simple enough that the game can be completely analyzed. You’ll use Nim to explore the minimax algorithm, which is able to play the game perfectly. This means that a minimax player will always win the game if at all possible.
Get to Know the Minimax Algorithm
Games have been a fertile ground for inventing and testing artificial intelligence algorithms. Games are well suited to this kind of research because of their clearly defined rules. One of the most famous algorithms is minimax. The name describes how one player tries to maximize their score while the other player tries to minimize it.
Minimax can be applied to many different games and more general decisions. In this tutorial, you’ll learn how to teach minimax to play Nim. However, you can use the same principles in other games, like tic-tac-toe and chess, as well.
Explore Game Trees
Recall the game that Mindy and Maximillian played in the previous section. The following table shows all the moves of the game:
| Mindy | Pile | Maximillian |
|---|---|---|
| 🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙 | ||
| 🪙🪙 | 🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙 | |
| 🪙🪙🪙🪙🪙🪙🪙🪙🪙 | 🪙 | |
| 🪙🪙🪙 | 🪙🪙🪙🪙🪙🪙 | |
| 🪙🪙🪙🪙 | 🪙🪙 | |
| 🪙🪙🪙 | 🪙 | |
| 🪙 |
This representation of the game explicitly shows how many counters each player removed on their turn. However, there’s some redundant information in the table. You can represent the same game by only keeping track of the number of counters in the pile and whose turn it is:
| Player to move | Pile |
|---|---|
| Mindy | 🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙 (12) |
| Maximillian | 🪙🪙🪙🪙🪙🪙🪙🪙🪙🪙 (10) |
| Mindy | 🪙🪙🪙🪙🪙🪙🪙🪙🪙 (9) |
| Maximillian | 🪙🪙🪙🪙🪙🪙 (6) |
| Mindy | 🪙🪙🪙🪙 (4) |
| Maximillian | 🪙 (1) |
While the number of counters each player removed on their turn isn’t explicitly spelled out, you can work it out by comparing the number of counters in the pile before and after a turn.
This representation is more compact. However, you can even eschew the table altogether and represent the game as a list of numbers: 12-10-9-6-4-1, Mindy starting. You’ll refer to each of these numbers as a game state.
You now have some notation to talk about different games. Next, turn your attention to possible strategies for winning the game. For example, could Maximillian have secured a win when he had six counters left in the pile?
One advantage of studying Simple-Nim is that the game tree isn’t forbiddingly large. The game tree describes all the valid moves in a game. Starting from a pile of six counters, there are only thirteen possible different games that can be played:
| Maximillian | Mindy | Maximillian | Mindy | Maximillian | Mindy | Maximillian |
|---|---|---|---|---|---|---|
| 6🪙 | 3🪙 | 1🪙 | 0 | |||
| 6🪙 | 3🪙 | 2🪙 | 1🪙 | 0 | ||
| 6🪙 | 4🪙 | 1🪙 | 0 | |||
| 6🪙 | 4🪙 | 2🪙 | 1🪙 | 0 | ||
| 6🪙 | 4🪙 | 3🪙 | 1🪙 | 0 | ||
| 6🪙 | 4🪙 | 3🪙 | 2🪙 | 1🪙 | 0 | |
| 6🪙 | 5🪙 | 2🪙 | 1🪙 | 0 | ||
| 6🪙 | 5🪙 | 3🪙 | 1🪙 | 0 | ||
| 6🪙 | 5🪙 | 3🪙 | 2🪙 | 1🪙 | 0 | |
| 6🪙 | 5🪙 | 4🪙 | 1🪙 | 0 | ||
| 6🪙 | 5🪙 | 4🪙 | 2🪙 | 1🪙 | 0 | |
| 6🪙 | 5🪙 | 4🪙 | 3🪙 | 1🪙 | 0 | |
| 6🪙 | 5🪙 | 4🪙 | 3🪙 | 2🪙 | 1🪙 | 0 |
Each column in the table represents a move, and each row represents one of the thirteen different games. The numbers in the table show how many counters are in the pile before the player makes their move. The bolded rows are those games that Maximillian would win.
Note: Technically speaking, there are a few more possible games than what’s listed in the table. For example, 6-3 is a valid game where Mindy takes the final three counters to immediately lose the game. But in this analysis, you’ll only consider games that end with the pile reduced to one counter that one player is forced to remove, as you can reasonably assume that a player wouldn’t make a losing move unless they had to.
For example, the first row in the table represents the game 6-3-1, which is won by Mindy, while the last row represents 6-5-4-3-2-1, where each player only takes one counter on their turn. The table shows all the possible games, but an even more insightful representation is a game tree showing all the possible outcomes:

In the figure, Maximillian’s turns are indicated by a darker background. The colored nodes are the leaves in the tree. They represent that the game has come to an end with zero counters left in play. Games that end at red nodes are won by Mindy, while those that end at green nodes are won by Maximillian.
You can find the same thirteen games in the tree as in the table. Start at the top of the tree and follow the branches until you arrive at a leaf node marked 0. Each level represents a move to a new game state. You can find the 6-3-1 game by following the leftmost branches, and 6-5-4-3-2-1 by descending to the far right.
Maximillian wins seven of the thirteen games, while Mindy wins the other six. This seems like the players should have an almost equal chance to win. Still, is there a way that Maximillian can ensure victory?
Find the Optimal Next Move
Rephrase the question above as follows: can Maximillian make a move such that he can win no matter what Mindy plays next? With the help of the tree above, you can work out what happens for each of Maximillian’s possible first moves:
- Take three counters and leave three counters in the pile: In this case, Mindy can take two counters and force Maximillian to lose the game.
- Take two counters and leave four counters in the pile: In this case, Mindy can take three counters and force Maximillian to lose the game.
- Take one counter and leave five counters in the pile: In this case, Mindy doesn’t have an immediate winning move. Instead, Maximillian has a winning move for each of Mindy’s choices.
If Maximillian takes one counter and leaves five in the pile, he can ensure victory!
This kind of argument forms the basis of the minimax algorithm. You’ll give each of the two players the role of either the maximizing player or the minimizing player. The current player wants to make a move to maximize their chance of winning, while their opponent wants to counter with a move to minimize the current player’s winning chances. In the example, Maximillian is the maximizing player, and Mindy is the minimizing player.
To keep track of the game, draw the tree of all possible moves. You’ve already done this for Simple-Nim starting with six counters. Then, assign a minimax score to all leaf nodes of the tree. In Simple-Nim, these are the nodes with zero counters left. The score will depend on the outcome represented by the leaf node.
If the maximizing player won the game, give the leaf a score of +1. Similarly, if the minimizing player won the game, score the leaf -1:
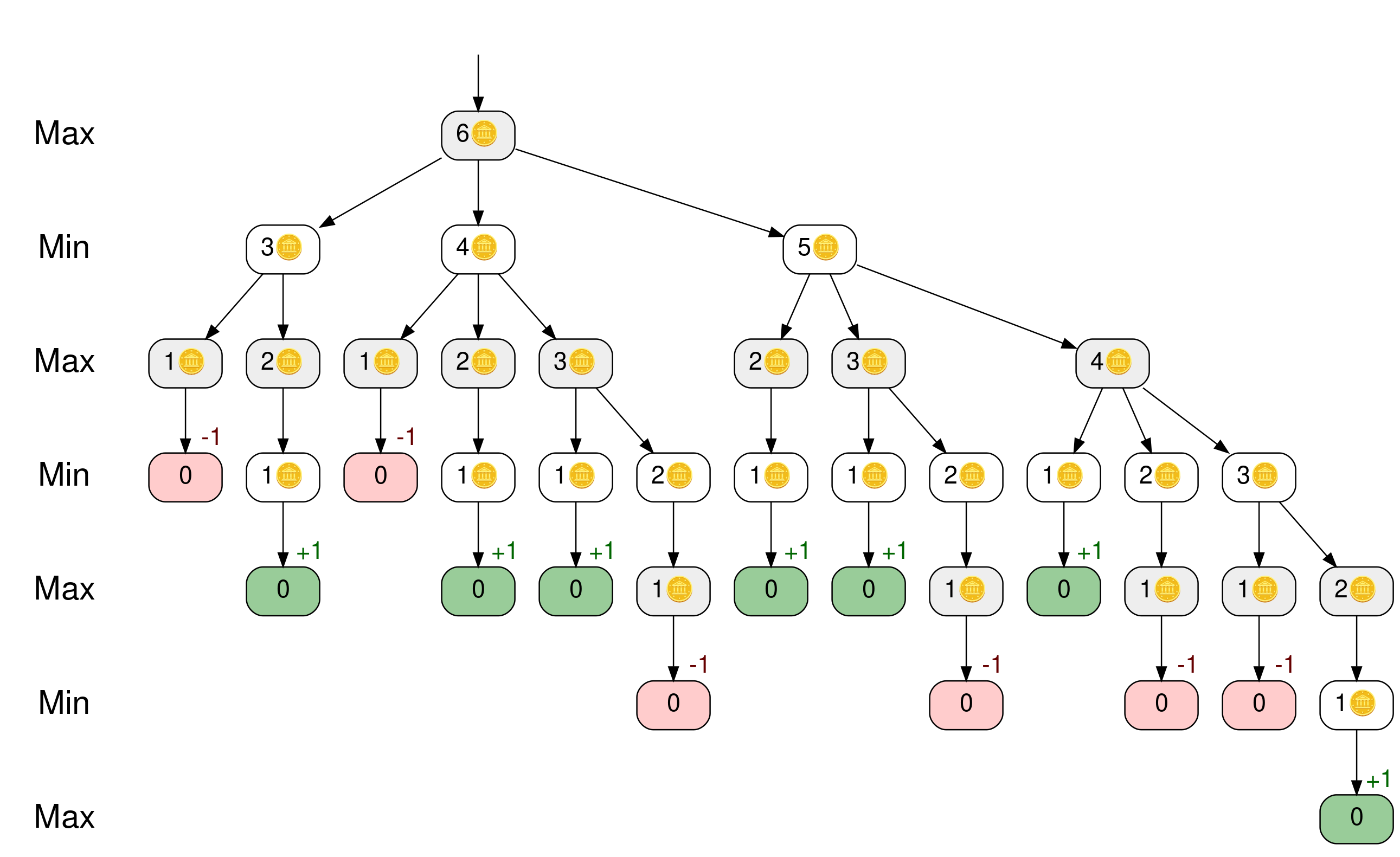
The leaf nodes in rows marked Max—Maximillian, the maximizing player—are marked by +1, while the leaf nodes in Mindy’s rows are marked by -1. Next, let the minimax scores bubble up the tree. Consider a node where all children have been assigned a score. If the node is on a Max row, then give it the maximum score of its children. Otherwise, give it the minimum score of its children.
If you do so for all the nodes in the tree, then you’ll end up with the following tree:
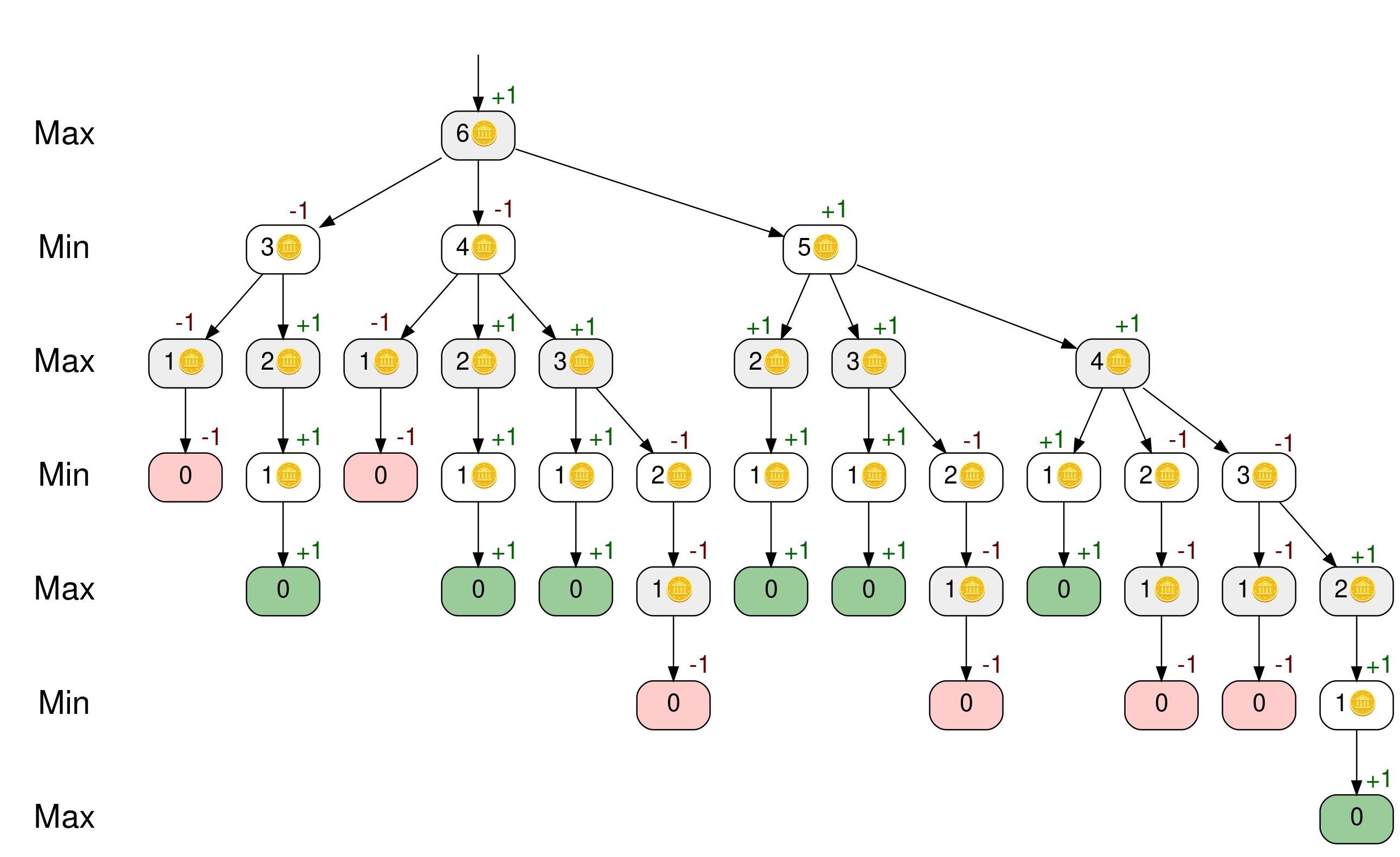
Because 6🪙, the top node of the tree, has a positive score, Maximillian can win the game. You can look at the children of the top node to find his best move. Both the 3🪙 and 4🪙 nodes have a score of -1, representing a win for Mindy. Maximillian should leave five counters, as the 5🪙 node is the only child of the top node that has a score of +1.
While you only use minimax scores of -1 and +1 when optimizing for Nim, you can use any range of numbers in general. For example, you may want to use -1, 0, and +1 when analyzing games like tic-tac-toe that can end in a tie.
Many games, including chess, have so many different possible moves that it’s not feasible to calculate the whole game tree. In those cases, you’ll only draw the tree to a certain depth and score the leaf nodes in this truncated tree. As those games aren’t over, you can’t score the leaves based on the final outcome of the game. Instead, you’ll score them based on some evaluation of the current position.
In the next section, you’ll use Python to calculate minimax scores.
Lose the Game of Nim Against a Python Minimax Player
You’ve gotten to know the steps of the minimax algorithm. In this section, you’ll implement minimax in Python. You’ll start by tailoring the algorithm directly to the game of Simple-Nim. Later, you’ll refactor your code to separate the core of the algorithm from the rules of the game, such that you can later apply your minimax code to other games.
Implement a Nim-Specific Minimax Algorithm
Consider the same example as in the previous section: it’s Maximillian’s turn, and there are six counters on the table. You’ll use the minimax algorithm to confirm that Maximillan can win this game and to calculate his next move.
First, though, consider a few examples of late-game situations. Assume it’s Maximillian’s turn and he sees the following game situation:
- Zero counters means that Mindy has already taken the last counter. Maximillian wins the game.
- One counter doesn’t leave any choice for Maximillian. He takes the counter, which leaves zero counters for Mindy. Using the same logic as in the previous bullet point but with the players’ roles reversed, you see that Mindy wins the game.
- Two counters gives Maximillian a choice. He can take one or two counters, which will leave Mindy with one or zero counters, respectively. Redo the logic from the previous bullet points from Mindy’s point of view. You’ll note that if Maximillian takes one counter, he leaves one counter and will win the game. If he takes two counters, he leaves zero counters, and Mindy wins the game.
Note how you reuse logic from earlier bullet points to figure out who can win from a particular game position. Now start to implement the logic in Python. Create a file named minimax_simplenim.py. You’ll use state to represent the number of counters and max_turn to keep track of whether it’s Maximillian’s turn or not.
The first rule, for zero counters, can be implemented as a conditional if test. You return 1 if Maximillian wins the game and -1 if he loses:
# minimax_simplenim.py
def minimax(state, max_turn):
if state == 0:
return 1 if max_turn else -1
# ...
Next, think about how to deal with game situations with one or more counters. They reduce to one or more states with fewer counters, where the opposite player moves first. For example, if it’s currently Maximillian’s turn, consider the outcomes of his possible moves and choose the best one:
# minimax_simplenim.py
def minimax(state, max_turn):
if state == 0:
return 1 if max_turn else -1
possible_new_states = [
state - take for take in (1, 2, 3) if take <= state
]
if max_turn:
scores = [
minimax(new_state, max_turn=False)
for new_state in possible_new_states
]
return max(scores)
# ...
You’ll first enumerate the possible new states, making sure that the players won’t take more counters than are available. You calculate the scores of Maximillian’s possible moves by calling minimax() again, noting that it’ll be Mindy’s turn next. Because Maximillian is the maximizing player, you’ll return the maximum of his possible scores.
Similarly, if it’s currently Mindy’s turn, consider her possible choices. Since -1 indicates that she’s winning, she’ll pick the outcome with the smallest score:
# minimax_simplenim.py
def minimax(state, max_turn):
if state == 0:
return 1 if max_turn else -1
possible_new_states = [
state - take for take in (1, 2, 3) if take <= state
]
if max_turn:
scores = [
minimax(new_state, max_turn=False)
for new_state in possible_new_states
]
return max(scores)
else:
scores = [
minimax(new_state, max_turn=True)
for new_state in possible_new_states
]
return min(scores)
The minimax() function continuously calls itself until it reaches the end of each game. In other words, minimax() is a recursive function.
Note: Implementing a recursive function is an intuitive way to traverse trees because exploring a branch of a tree is the same operation as exploring the bigger tree.
However, recursive functions have some problems, in particular for bigger trees. In Python, function calls have some overhead, and the call stack is limited.
You’ll see how to counter some of these issues later. But a non-recursive implementation of minimax may be a better option if you need to optimize the minimax algorithm for speed.
First, confirm that minimax() works as expected. Open a Python REPL and import your function:
>>> from minimax_simplenim import minimax
>>> minimax(6, max_turn=True)
1
>>> minimax(5, max_turn=False)
1
>>> minimax(4, max_turn=False)
-1
You first confirm that Maximillian can win if he plays with six counters left, as represented by 1. Similarly, Maximillian can still win if he leaves five counters for Mindy. If instead he leaves four counters for Mindy, then she will win.
To effectively find which move Maximillian should play next, you can do the same calculations in a loop:
>>> state = 6
>>> for take in (1, 2, 3):
... new_state = state - take
... score = minimax(new_state, max_turn=False)
... print(f"Move from {state} to {new_state}: {score}")
...
Move from 6 to 5: 1
Move from 6 to 4: -1
Move from 6 to 3: -1
Looking for the highest score, you see that Maximillian should take one counter and leave five on the table. Next, take this one step further and create a function that can find Maximillian’s best move:
# minimax_simplenim.py
# ...
def best_move(state):
for take in (1, 2, 3):
new_state = state - take
score = minimax(new_state, max_turn=False)
if score > 0:
break
return score, new_state
You loop until you find a move that gives a positive score—in effect, a score of 1. You may also loop through all three possible moves without finding a winning move. To indicate this, you return both the score and the best move:
>>> best_move(6)
(1, 5)
>>> best_move(5)
(-1, 2)
Testing your function, you confirm that when faced with six counters, Maximillian can win the game by removing one counter and leaving five for Mindy. If there are five counters on the table, all moves have a score of -1. Even though all moves are equally bad, best_move() suggests the last move that it checked: take three counters and leave two.
Look back at your code for minimax() and best_move(). Both functions contain logic that deals with the minimax algorithm and logic that deals with the rules of Simple-Nim. In the next subsection, you’ll see how you can separate these.
Refactor to a General Minimax Algorithm
You’ve coded the following rules of Simple-Nim into your minimax algorithm:
- A player can take one, two, or three counters on their turn.
- A player can’t take more counters than are left in the game.
- The game is over when there are zero counters left.
- The player who takes the last counter loses the game.
Additionally, you’ve used max_turn to keep track of whether Maximillian is the active player or not. To be more general, you can think of the current player as the one who wants to maximize their score. To indicate this, you’ll replace the max_turn flag with is_maximizing.
Start rewriting your code by adding two new functions:
# minimax_simplenim.py
# ...
def possible_new_states(state):
return [state - take for take in (1, 2, 3) if take <= state]
def evaluate(state, is_maximizing):
if state == 0:
return 1 if is_maximizing else -1
These two functions implement the rules of Simple-Nim. With possible_new_states(), you calculate the possible next states while making sure that a player can’t take more counters than those available on the board.
You evaluate a game position with evaluate(). If there are no counters left, then the function returns 1 if the maximizing player won the game and -1 if the other—minimizing—player won. If the game isn’t over, execution will continue to the end of the function and implicitly return None.
You can now rewrite minimax() to refer to possible_new_states() and evaluate():
# minimax_simplenim.py
def minimax(state, is_maximizing):
if (score := evaluate(state, is_maximizing)) is not None:
return score
if is_maximizing:
scores = [
minimax(new_state, is_maximizing=False)
for new_state in possible_new_states(state)
]
return max(scores)
else:
scores = [
minimax(new_state, is_maximizing=True)
for new_state in possible_new_states(state)
]
return min(scores)
Remember to also rename max_turn to is_maximizing.
You only score a game state if there are zero counters left and the winner has been decided. Therefore, you need to check whether score is None to decide if you should continue to call minimax() or return the game evaluation. You use an assignment expression (:=) to both check and remember the evaluated game score.
Next, observe that the blocks in your if … else statement are quite similar. The only differences between the blocks are which function, max() or min(), you use to find the best score and what value you use for is_maximizing in the recursive calls to minimax(). Both of these can be directly calculated from the current value of is_maximizing.
You can therefore collapse the if … else block into one statement:
# minimax_simplenim.py
def minimax(state, is_maximizing):
if (score := evaluate(state, is_maximizing)) is not None:
return score
return (max if is_maximizing else min)(
minimax(new_state, is_maximizing=not is_maximizing)
for new_state in possible_new_states(state)
)
You use a conditional expression to call either max() or min(). To reverse the value of is_maximizing, you pass not is_maximizing to the recursive calls to minimax().
The code for minimax() is now quite compact. More importantly, the rules of Simple-Nim aren’t explicitly encoded within the algorithm. Instead, they’re encapsulated in possible_new_states() and evaluate().
You finish the refactoring by also expressing best_move() in terms of possible_new_states() and with is_maximizing instead of max_turn:
# minimax_simplenim.py
# ...
def best_move(state):
for new_state in possible_new_states(state):
score = minimax(new_state, is_maximizing=False)
if score > 0:
break
return score, new_state
As before, you check the outcome of each possible move and return the first that guarantees a win.
Note: There’s no error handling in best_move(). In particular, it assumes that possible_new_states() returns at least one new game state. If it doesn’t, then the loop won’t run at all, and score and new_state will be undefined.
This means that you should only call best_move() with a valid game state. Alternatively, you can add an extra check inside best_move() itself.
In Python, tuples are compared element by element. You can take advantage of this to use max() directly instead of checking the possible moves explicitly:
# minimax_simplenim.py
# ...
def best_move(state):
return max(
(minimax(new_state, is_maximizing=False), new_state)
for new_state in possible_new_states(state)
)
As earlier, you consider—and return—a tuple containing the score and the best new state. Because comparisons, including max(), are done element by element in tuples, the score must be the first element in the tuple.
You’re still able to find the optimal moves:
>>> best_move(6)
(1, 5)
>>> best_move(5)
(-1, 4)
As before, best_move() suggests that you should take one counter if you’re faced with six. In the losing situation of five counters, it doesn’t matter how many counters you take, because you’re about to lose anyway. Your implementation based on max() ends up leaving as many counters on the table as possible.
You can expand the box below to see the full source code that you’ve implemented in this section:
You’ve encapsulated the rules of Simple-Nim in possible_new_states() and evaluate(). These functions are used by minimax() and best_move():
# minimax_simplenim.py
def minimax(state, is_maximizing):
if (score := evaluate(state, is_maximizing)) is not None:
return score
return (max if is_maximizing else min)(
minimax(new_state, is_maximizing=not is_maximizing)
for new_state in possible_new_states(state)
)
def best_move(state):
return max(
(minimax(new_state, is_maximizing=False), new_state)
for new_state in possible_new_states(state)
)
def possible_new_states(state):
return [state - take for take in (1, 2, 3) if take <= state]
def evaluate(state, is_maximizing):
if state == 0:
return 1 if is_maximizing else -1
Use best_move() to find the next move in a given game.
Great job! You’ve implemented a minimax algorithm for Simple-Nim. To challenge it, you should play a few games against your code. Start with some number of counters and take turns removing counters yourself and using best_move() to choose how many counters your virtual opponent will remove. Unless you play a perfect game, you’ll lose!
In the next section, you’ll implement the same algorithm for the regular rules of Nim.
Have Fun With Nim Variants
So far, you’ve played and implemented Simple-Nim. In this section, you’ll learn the most common rules of Nim. This’ll add some more variety to your games.
Nim—with its regular rules—is still a simple game. But it’s also a surprisingly foundational game. It turns out that a family of games called impartial games are all essentially Nim in disguise.
Play the Regular Game of Nim
It’s time to pull out the regular rules of Nim. You can still recognize the game, but it allows the players a bit more choice:
- There are several piles, with a number of counters in each.
- Two players take alternating turns.
- On their turn, a player removes as many counters as they want, but the counters must come from the same pile.
- The player that takes the last counter loses the game.
Note that there’s no longer any restriction on how many counters to remove on a turn. If a pile contains twenty counters, then the current player may take all of them.
As an example, consider a game starting with three piles containing two, three, and five counters, respectively. Have a look at your friends Mindy and Maximillian playing the game:
- Mindy takes four counters from the third pile, leaving two, three, and one counters.
- Maximillian takes two counters from the second pile, leaving two, one, and one counters.
- Mindy takes one counter from the first pile, leaving one, one, and one counters.
- Maximillian doesn’t have any interesting choices left but takes one counter from the third pile, leaving one, one, and zero counters.
- Mindy takes one counter from the second pile, leaving one, zero, and zero counters.
- Maximillian takes the last remaining counter and loses the game.
You can represent the game in a table:
| Player to move | Pile one | Pile two | Pile three |
|---|---|---|---|
| Mindy | 🪙🪙 | 🪙🪙🪙 | 🪙🪙🪙🪙🪙 |
| Maximillian | 🪙🪙 | 🪙🪙🪙 | 🪙 |
| Mindy | 🪙🪙 | 🪙 | 🪙 |
| Maximillian | 🪙 | 🪙 | 🪙 |
| Mindy | 🪙 | 🪙 | |
| Maximillian | 🪙 |
As in the Simple-Nim game, Maximillian takes the last counter, so Mindy wins.
Note: You should play a few games of Nim to get a feel for how the new rules change the strategy. Try it with a different number of piles, say three, four, or five. You don’t need a lot of counters in each pile. Between three and nine is a good starting point.
Think about how you can implement the minimax algorithm for these new rules. Remember that you only need to reimplement possible_new_states() and evaluate().
Adapt Your Code to Regular Nim
First, copy your code in minimax_simplenim.py to a new file named minimax_nim.py. Then, consider how you can list all the possible moves from a given game state. For example, Mindy and Maximillian started with two, three, and five counters. You can list all the possible next states as follows:
| Pile one: 🪙🪙 | Pile two: 🪙🪙🪙 | Pile three: 🪙🪙🪙🪙🪙 |
|---|---|---|
| 🪙🪙🪙 | 🪙🪙🪙🪙🪙 | |
| 🪙 | 🪙🪙🪙 | 🪙🪙🪙🪙🪙 |
| 🪙🪙 | 🪙🪙🪙🪙🪙 | |
| 🪙🪙 | 🪙 | 🪙🪙🪙🪙🪙 |
| 🪙🪙 | 🪙🪙 | 🪙🪙🪙🪙🪙 |
| 🪙🪙 | 🪙🪙🪙 | |
| 🪙🪙 | 🪙🪙🪙 | 🪙 |
| 🪙🪙 | 🪙🪙🪙 | 🪙🪙 |
| 🪙🪙 | 🪙🪙🪙 | 🪙🪙🪙 |
| 🪙🪙 | 🪙🪙🪙 | 🪙🪙🪙🪙 |
There are ten possible moves. You can take one or two counters from the first pile; one, two, or three counters from the second pile; or one, two, three, four, or five counters from the third pile.
In code, you can list all the possible new states with a nested loop. The outer loop will consider each pile in turn, and the inner loop will iterate over the different choices for each pile:
# minimax_nim.py
# ...
def possible_new_states(state):
for pile, counters in enumerate(state):
for remain in range(counters):
yield state[:pile] + (remain,) + state[pile + 1 :]
Here, you’re representing the game state as a tuple of numbers, with each number representing the number of counters in a pile. For example, the situation above is represented as (2, 3, 5). You then loop over each of the piles, using enumerate() to keep track of the index of the current pile.
For each pile, you use range() to list all the possible choices of how many counters can remain in that pile. You return a new game state by copying state except for the current pile. Recall that tuples can be sliced with square brackets ([]) and concatenated with the plus sign (+).
Instead of collecting the possible moves in a list, you use yield to send them back one at a time. This makes possible_new_states() a generator:
>>> from minimax_nim import possible_new_states
>>> possible_new_states((2, 3, 5))
<generator object possible_new_states at 0x7f1516ebc660>
>>> list(possible_new_states((2, 3, 5)))
[(0, 3, 5), (1, 3, 5), (2, 0, 5), (2, 1, 5), (2, 2, 5),
(2, 3, 0), (2, 3, 1), (2, 3, 2), (2, 3, 3), (2, 3, 4)]
Just calling possible_new_states() returns a generator without generating the possible new states. You can see the moves by converting the generator to a list.
To implement evaluate() for regular Nim, you need to consider two questions:
- How to detect that the game is over
- How to score the game when it’s over
The rules for winning Nim are the same as for Simple-Nim, so you can score the game the same as earlier. The game is over when all the piles are empty. On the other hand, if any pile still contains at least one counter, then the game isn’t over. You use all() to check that all piles contain zero counters:
# minimax_nim.py
# ...
def evaluate(state, is_maximizing):
if all(counters == 0 for counters in state):
return 1 if is_maximizing else -1
If the game is over, then you score the game 1 if the maximizing player has won the game and -1 if the minimizing player has won. As before, you implicitly return None if the game isn’t over and you can’t yet evaluate the game state.
Because you’ve coded all the game rules in possible_new_states() and evaluate(), you don’t need to make any changes to minimax() or best_move(). You may expand the box below to see the full source code needed for regular Nim:
The following code can calculate the next optimal move in regular Nim:
# minimax_nim.py
def minimax(state, is_maximizing):
if (score := evaluate(state, is_maximizing)) is not None:
return score
return (max if is_maximizing else min)(
minimax(new_state, is_maximizing=not is_maximizing)
for new_state in possible_new_states(state)
)
def best_move(state):
return max(
(minimax(new_state, is_maximizing=False), new_state)
for new_state in possible_new_states(state)
)
def possible_new_states(state):
for pile, counters in enumerate(state):
for remain in range(counters):
yield state[:pile] + (remain,) + state[pile + 1 :]
def evaluate(state, is_maximizing):
if all(counters == 0 for counters in state):
return 1 if is_maximizing else -1
There are no changes in minimax() and best_move() as compared to minimax_simplenim.py.
You can use your code to check if Mindy chose a good first move in the example at the beginning of this section:
>>> from minimax_nim import best_move
>>> best_move((2, 3, 5))
(1, (2, 3, 1))
>>> best_move((2, 3, 1))
(-1, (2, 3, 0))
Indeed, taking four counters from the third pile is an optimal move for Mindy. In the situation where there are two, three, and one counters in the piles, there’s no optimal move, as indicated by the score of -1.
You’ve seen that you can reuse minimax() and best_move() as you change the rules of Nim.
Try Other Variants of Nim
Nim is sometimes called a misère game because the goal is to avoid taking the last counter. A popular variant of Nim changes the winning condition. In this variant, the player that takes the last counter wins the game. How would you change your code to play this version of the game?
Try to implement the minimax algorithm for the non-misère variant of Nim. You only need to change one line of code.
To modify your code such that it optimizes for taking the last counter, you change how you evaluate the game:
def evaluate(state, is_maximizing):
if all(counters == 0 for counters in state):
return -1 if is_maximizing else 1
Now, if there are no counters left, the player who made the last move has already won the game. To indicate this, you return the worst possible score: -1 if you’re maximizing and 1 if you’re minimizing.
Another variant of Nim starts with all the counters in one pile:
- There are several counters, all starting in one pile.
- Two players take alternating turns.
- On their turn, a player splits a pile in two, such that the two new piles have different numbers of counters.
- The first player that can’t split any pile loses the game.
In this variant, each move creates a new pile. The game lasts until all the piles contain one or two counters, because those piles can’t be split.
Consider a game starting from a pile of six counters. Note that there are two possible starting moves: split to either five-one or four-two. Three-three isn’t a legal move, because the two new piles must have different numbers of counters. Watch Mindy and Maximillian play the game:
- Mindy splits the pile into two piles, with four and two counters, respectively.
- Maximillian splits the first pile so there are three piles, with three, one, and two counters.
- Mindy splits the first pile so there are four piles, with two, one, one, and two counters.
- Maximillian can’t split any pile, because they all contain one or two counters, so he loses the game.
Mindy wins the game because Maximillian isn’t able to make a move. How would you implement a version of minimax that can find the best move in this variant?
Implement the rules for the Nim variant where players take turns splitting the piles of counters. There are four questions that you should think about:
- How should you represent the game state?
- How can you enumerate the possible new states after a move?
- How can you detect that the game is over?
- How should you evaluate the outcome of a finished game?
You need to create new possible_new_states() and evaluate() functions.
Make a copy of your minimax_nim.py file and name it minimax_nim_split.py. You can then modify possible_new_states() and evaluate() to take the new rules into account:
# minimax_nim_split.py
# ...
def possible_new_states(state):
for pile, counters in enumerate(state):
for take in range(1, (counters + 1) // 2):
yield state[:pile] + (counters - take, take) + state[pile + 1 :]
def evaluate(state, is_maximizing):
if all(counters <= 2 for counters in state):
return -1 if is_maximizing else 1
To list the possible new states, you consider each pile in turn. You need to think about how you can split a pile of counters.
Note that splits are symmetrical. You don’t need to split a pile of 3 counters into both (1, 2) and (2, 1). This means that you can iterate up to approximately half the number of counters in the pile.
More precisely, you iterate over range(1, (counters + 1) // 2). This implicitly takes into account that you must split a pile into two piles with different numbers of counters. For example, both 5 and 6 counters let take take the values 1 and 2. The split pile is represented by the tuple (counters - take, take).
You only evaluate the end states of the game. The game is over when all the piles contain one or two counters. When the game is over, the current player has lost, as they can’t make another move.
There are many other variants of Nim. Have fun implementing some of those as well.
Optimize Minimax With Alpha-Beta Pruning
One challenge with the minimax algorithm is that the game trees can be huge. The number of nodes in the tree representing Simple-Nim follows a Fibonacci-like formula. For example, the number of children of a node representing six counters is the sum of the nodes in the trees representing three, four, and five counters.
These numbers grow quickly, as the following table shows:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | 25 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 6 | 12 | 22 | 41 | 76 | 4,434,690 |
To represent a game starting with twenty-five counters, you’ll need a tree with more than four million nodes. If you try to calculate minimax(25, True), you’ll notice that it takes a few seconds.
In Simple-Nim, the game tree consists of many repeated game states. For example, you can move from six to three counters in four different ways: 6-3, 6-4-3, 6-5-3, and 6-5-4-3. Therefore, the same game states are calculated repeatedly by minimax(). You can counter this by using a cache:
from functools import cache
@cache
def minimax(state, is_maximizing):
# ...
This will speed up your code significantly, as Python only calculates the minimax score for each game state once.
Note: In regular Nim, there are many equivalent game states. For example, (2, 2, 3), (2, 3, 2), and (3, 2, 2) all represent the same position. One optimization that you can do to keep the game tree smaller is to only list one of each symmetrical position in possible_new_states(). You won’t cover this right now, but try to add it yourself and share your experience in the comments!
Another way to make your algorithm more efficient is to avoid unnecessarily exploring subtrees. In this section, you’ll learn about alpha-beta pruning, which you can use to cut down the size of your game tree.
Prune Your Game Trees
Assume that you’re playing Simple-Nim and there are three counters left. You have two options to consider—leaving one or leaving two counters:
- If you leave one counter, then your opponent needs to take it, and you’ll win the game.
- You don’t need to calculate the outcome of leaving two counters, because you’ve already found a move that’ll win you the game.
In this argument, you didn’t need to figure out whether you should leave two counters. You’ve pruned the game tree.
Now return to the example where it’s Maximillian’s turn with six counters on the table. If you consider branches from left to right and stop exploring subtrees once the minimax score of a node is decided, then you’ll end up with the following tree:
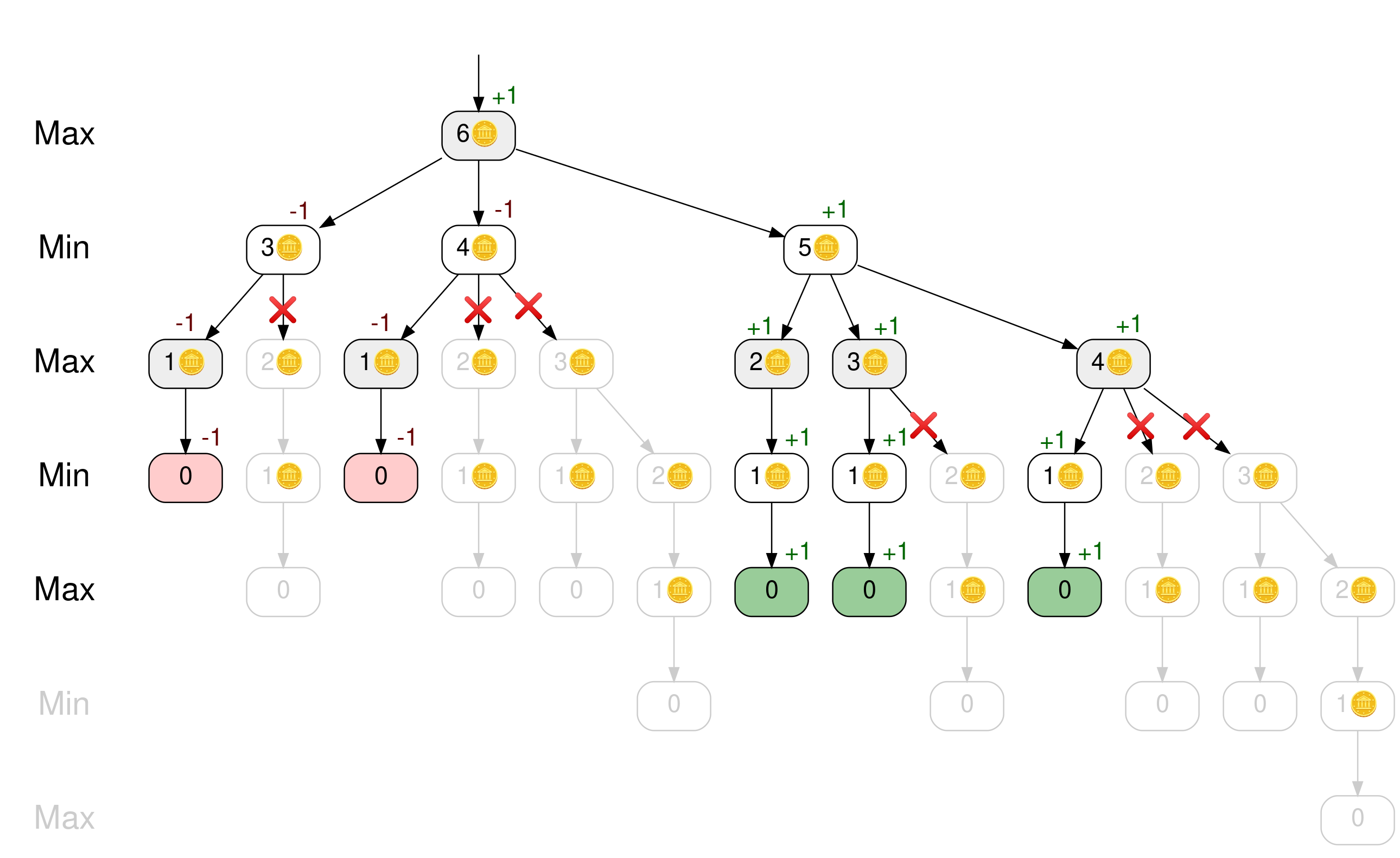
The game tree becomes much smaller. The original tree had forty-one nodes, while this pruned version only needs seventeen nodes to represent all the moves in the game.
This procedure is called alpha-beta pruning because it uses two parameters, α and β, to keep track of when a branch can be cut. In the next section, you’ll rewrite minimax() to use alpha-beta pruning.
Implement Alpha-Beta Pruning
You can add alpha-beta pruning to your code by refactoring the minimax() function. You’ve already refactored minimax() such that the same implementation works for all your variants of Nim. In the previous subsection, you pruned the tree for Simple-Nim. However, you might as well implement alpha-beta pruning for regular Nim. Make a copy of minimax_nim.py and call it alphabeta_nim.py.
You need a criterion to know when you can stop exploring. To do so, you’ll add two parameters, alpha and beta:
alphawill represent the minimum score that the maximizing player is ensured.betawill represent the maximum score that the minimizing player is ensured.
If beta is ever smaller than or equal to alpha, then the player can stop exploring that game tree. The maximizing will already have found a better option than the player could find by exploring further.
To implement this idea, you’ll start by replacing your comprehension with an explicit for loop. You need the explicit loop so that you can break out of it and effectively prune the tree:
# alphabeta_nim.py
from functools import cache
@cache
def minimax(state, is_maximizing):
if (score := evaluate(state, is_maximizing)) is not None:
return score
scores = []
for new_state in possible_new_states(state):
scores.append(minimax(new_state, is_maximizing=not is_maximizing))
return (max if is_maximizing else min)(scores)
# ...
Here, you’re explicitly collecting the scores of child nodes in a list named scores before returning the optimal score.
Next, you’ll add alpha and beta as parameters. Theoretically, they should start at negative and positive infinity, respectively, to represent the worst possible scores for the two players. However, since the only possible scores in Nim are -1 and 1, you can use those as starting values.
For each minimax evaluation, you update the values of alpha and beta and compare them. Once beta becomes smaller than or equal to alpha, you break out of the loop, as you don’t need to consider any further moves:
# alphabeta_nim.py
from functools import cache
@cache
def minimax(state, is_maximizing, alpha=-1, beta=1):
if (score := evaluate(state, is_maximizing)) is not None:
return score
scores = []
for new_state in possible_new_states(state):
scores.append(
score := minimax(new_state, not is_maximizing, alpha, beta)
)
if is_maximizing:
alpha = max(alpha, score)
else:
beta = min(beta, score)
if beta <= alpha:
break
return (max if is_maximizing else min)(scores)
# ...
At the recursive step, you use an assignment expression (:=) to both store the return value of minimax() and add it to the list of scores.
Alpha-beta pruning is only an optimization. It doesn’t change the outcome of the minimax algorithm. You’ll still see the same results as earlier:
>>> from alphabeta_nim import best_move
>>> best_move((2, 3, 5))
(1, (2, 3, 1))
>>> best_move((2, 3, 1))
(-1, (2, 3, 0))
If you measure the time that the algorithm takes to execute, then you’ll notice that minimax is faster with alpha-beta pruning because it needs to explore less of the game tree.
You can expand the box below to see the full Python code for using minimax with alpha-beta pruning to find the optimal Nim move:
Alpha-beta pruning is implemented in minimax():
# alphabeta_nim.py
from functools import cache
@cache
def minimax(state, is_maximizing, alpha=-1, beta=1):
if (score := evaluate(state, is_maximizing)) is not None:
return score
scores = []
for new_state in possible_new_states(state):
scores.append(
score := minimax(new_state, not is_maximizing, alpha, beta)
)
if is_maximizing:
alpha = max(alpha, score)
else:
beta = min(beta, score)
if beta <= alpha:
break
return (max if is_maximizing else min)(scores)
def best_move(state):
return max(
(minimax(new_state, is_maximizing=False), new_state)
for new_state in possible_new_states(state)
)
def possible_new_states(state):
for pile, counters in enumerate(state):
for remain in range(counters):
yield state[:pile] + (remain,) + state[pile + 1 :]
def evaluate(state, is_maximizing):
if all(counters == 0 for counters in state):
return 1 if is_maximizing else -1
Call best_move() to find the optimal move from a given game state.
Even though minimax() now does alpha-beta pruning, it still relies on evaluate() and possible_new_states() to implement the rules of the game. You can therefore use your new minimax() implementation on Simple-Nim as well.
Conclusion
Great job! You’ve learned about the minimax algorithm and seen how you can use it to find the optimal moves in the game of Nim. While Nim is a simple game, minimax can be applied to many other games, like tic-tac-toe and chess. You can apply the principles that you’ve explored to many different games.
In this tutorial, you’ve learned how to:
- Explain the principles of the minimax algorithm
- Play several variations of the game of Nim
- Implement the minimax algorithm
- Lose the game of Nim against a minimax player
- Use alpha-beta pruning to optimize the minimax algorithm
Think about how you may be able to apply the minimax algorithm to your favorite game and how you would implement it in Python. In the comments, let your fellow programmers know which other games you’re losing against minimax.
Source Code: Click here to download the free source code that you’ll use to lose the game of Nim against your minimax player.






