Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Thinking Recursively in Python
“Of all ideas I have introduced to children, recursion stands out as the one idea that is particularly able to evoke an excited response.”
— Seymour Papert, Mindstorms

Problems (in life and also in computer science) can often seem big and scary. But if we keep chipping away at them, more often than not we can break them down into smaller chunks trivial enough to solve. This is the essence of thinking recursively, and my aim in this article is to provide you, my dear reader, with the conceptual tools necessary to approach problems from this recursive point of view.
Together, we’ll learn how to work with recursion in our Python programs by mastering concepts such as recursive functions and recursive data structures. We’ll also talk about maintaining state during recursion and avoiding recomputation by caching results. This is going to be a lot of fun. Onwards and upwards!
Dear Pythonic Santa Claus…
I realize that as fellow Pythonistas we are all consenting adults here, but children seem to grok the beauty of recursion better. So let’s not be adults here for a moment and talk about how we can use recursion to help Santa Claus.
Have you ever wondered how Christmas presents are delivered? I sure have, and I believe Santa Claus has a list of houses he loops through. He goes to a house, drops off the presents, eats the cookies and milk, and moves on to the next house on the list. Since this algorithm for delivering presents is based on an explicit loop construction, it is called an iterative algorithm.

The algorithm for iterative present delivery implemented in Python:
houses = ["Eric's house", "Kenny's house", "Kyle's house", "Stan's house"]
def deliver_presents_iteratively():
for house in houses:
print("Delivering presents to", house)
>>> deliver_presents_iteratively()
Delivering presents to Eric's house
Delivering presents to Kenny's house
Delivering presents to Kyle's house
Delivering presents to Stan's house
But I feel for Santa. At his age, he shouldn’t have to deliver all the presents by himself. I propose an algorithm with which he can divide the work of delivering presents among his elves:
- Appoint an elf and give all the work to him
- Assign titles and responsibilities to the elves based on the number of houses for which they are responsible:
> 1He is a manager and can appoint two elves and divide his work among them= 1He is a worker and has to deliver the presents to the house assigned to him
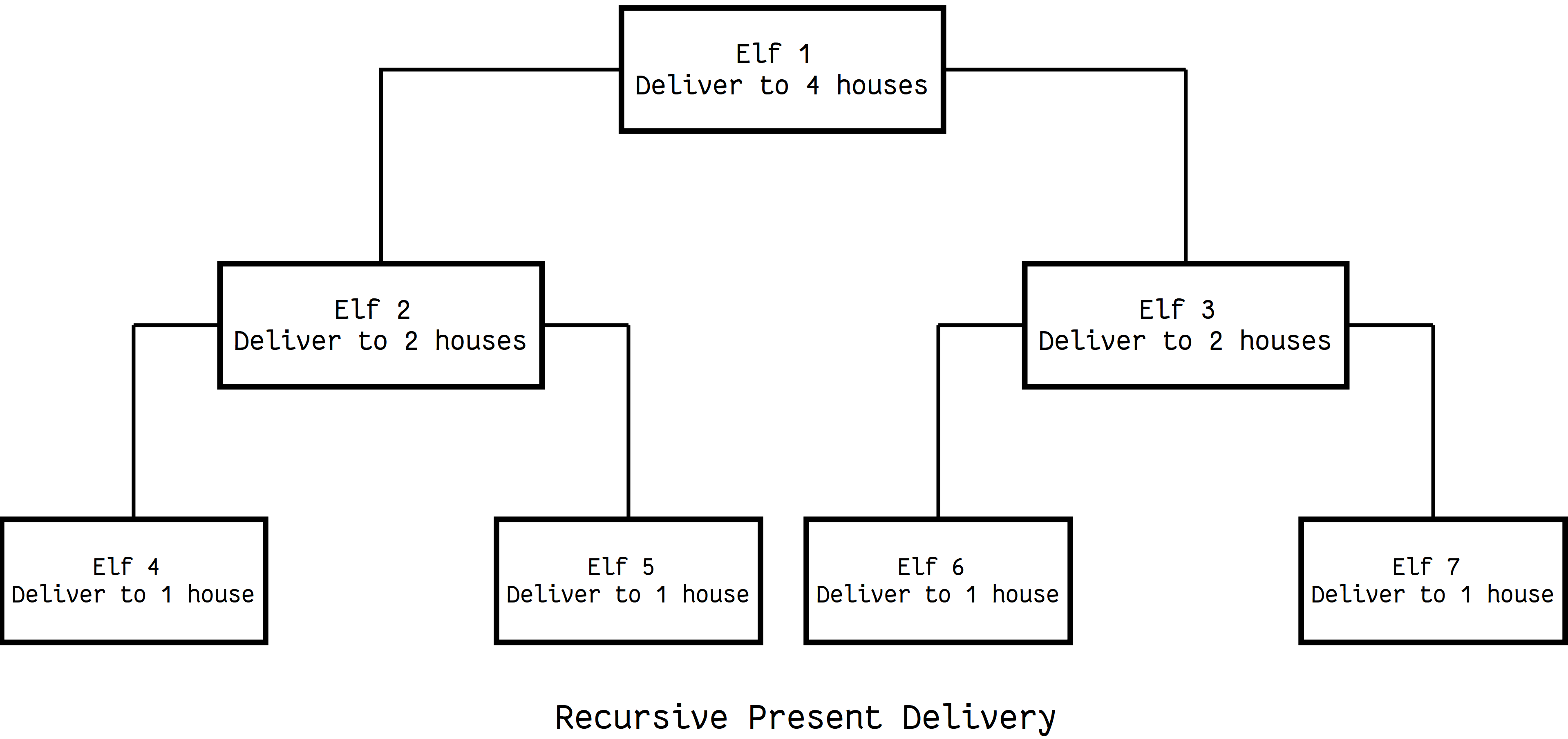
This is the typical structure of a recursive algorithm. If the current problem represents a simple case, solve it. If not, divide it into subproblems and apply the same strategy to them.
The algorithm for recursive present delivery implemented in Python:
houses = ["Eric's house", "Kenny's house", "Kyle's house", "Stan's house"]
# Each function call represents an elf doing his work
def deliver_presents_recursively(houses):
# Worker elf doing his work
if len(houses) == 1:
house = houses[0]
print("Delivering presents to", house)
# Manager elf doing his work
else:
mid = len(houses) // 2
first_half = houses[:mid]
second_half = houses[mid:]
# Divides his work among two elves
deliver_presents_recursively(first_half)
deliver_presents_recursively(second_half)
>>> deliver_presents_recursively(houses)
Delivering presents to Eric's house
Delivering presents to Kenny's house
Delivering presents to Kyle's house
Delivering presents to Stan's house
Recursive Functions in Python
Now that we have some intuition about recursion, let’s introduce the formal definition of a recursive function. A recursive function is a function defined in terms of itself via self-referential expressions.
This means that the function will continue to call itself and repeat its behavior until some condition is met to return a result. All recursive functions share a common structure made up of two parts: base case and recursive case.
To demonstrate this structure, let’s write a recursive function for calculating n!:
-
Decompose the original problem into simpler instances of the same problem. This is the recursive case:
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1 n! = n x (n−1)! -
As the large problem is broken down into successively less complex ones, those subproblems must eventually become so simple that they can be solved without further subdivision. This is the base case:
n! = n x (n−1)! n! = n x (n−1) x (n−2)! n! = n x (n−1) x (n−2) x (n−3)! ⋅ ⋅ n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2! n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1!
Here, 1! is our base case, and it equals 1.
Recursive function for calculating n! implemented in Python:
def factorial_recursive(n):
# Base case: 1! = 1
if n == 1:
return 1
# Recursive case: n! = n * (n-1)!
else:
return n * factorial_recursive(n-1)
>>> factorial_recursive(5)
120
Behind the scenes, each recursive call adds a stack frame (containing its execution context) to the call stack until we reach the base case. Then, the stack begins to unwind as each call returns its results:

Maintaining State
When dealing with recursive functions, keep in mind that each recursive call has its own execution context, so to maintain state during recursion you have to either:
- Thread the state through each recursive call so that the current state is part of the current call’s execution context
- Keep the state in global scope
A demonstration should make things clearer. Let’s calculate 1 + 2 + 3 ⋅⋅⋅⋅ + 10 using recursion. The state that we have to maintain is (current number we are adding, accumulated sum till now).
Here’s how you do that by threading it through each recursive call (i.e. passing the updated current state to each recursive call as arguments):
def sum_recursive(current_number, accumulated_sum):
# Base case
# Return the final state
if current_number == 11:
return accumulated_sum
# Recursive case
# Thread the state through the recursive call
else:
return sum_recursive(current_number + 1, accumulated_sum + current_number)
# Pass the initial state
>>> sum_recursive(1, 0)
55

Here’s how you maintain the state by keeping it in global scope:
# Global mutable state
current_number = 1
accumulated_sum = 0
def sum_recursive():
global current_number
global accumulated_sum
# Base case
if current_number == 11:
return accumulated_sum
# Recursive case
else:
accumulated_sum = accumulated_sum + current_number
current_number = current_number + 1
return sum_recursive()
>>> sum_recursive()
55
I prefer threading the state through each recursive call because I find global mutable state to be evil, but that’s a discussion for a later time.
Recursive Data Structures in Python
A data structure is recursive if it can be defined in terms of a smaller version of itself. A list is an example of a recursive data structure. Let me demonstrate. Assume that you have only an empty list at your disposal, and the only operation you can perform on it is this:
# Return a new list that is the result of
# adding element to the head (i.e. front) of input_list
def attach_head(element, input_list):
return [element] + input_list
Using the empty list and the attach_head operation, you can generate any list. For example, let’s generate [1, 46, -31, "hello"]:
attach_head(1, # Will return [1, 46, -31, "hello"]
attach_head(46, # Will return [46, -31, "hello"]
attach_head(-31, # Will return [-31, "hello"]
attach_head("hello", [])))) # Will return ["hello"]
[1, 46, -31, 'hello']

-
Starting with an empty list, you can generate any list by recursively applying the
attach_headfunction, and thus the list data structure can be defined recursively as:+---- attach_head(element, smaller list) list = + +---- empty list -
Recursion can also be seen as self-referential function composition. We apply a function to an argument, then pass that result on as an argument to a second application of the same function, and so on. Repeatedly composing
attach_headwith itself is the same asattach_headcalling itself repeatedly.
List is not the only recursive data structure. Other examples include set, tree, dictionary, etc.
Recursive data structures and recursive functions go together like bread and butter. The recursive function’s structure can often be modeled after the definition of the recursive data structure it takes as an input. Let me demonstrate this by calculating the sum of all the elements of a list recursively:
def list_sum_recursive(input_list):
# Base case
if input_list == []:
return 0
# Recursive case
# Decompose the original problem into simpler instances of the same problem
# by making use of the fact that the input is a recursive data structure
# and can be defined in terms of a smaller version of itself
else:
head = input_list[0]
smaller_list = input_list[1:]
return head + list_sum_recursive(smaller_list)
>>> list_sum_recursive([1, 2, 3])
6
Naive Recursion is Naive
The Fibonacci numbers were originally defined by the Italian mathematician Fibonacci in the thirteenth century to model the growth of rabbit populations. Fibonacci surmised that the number of pairs of rabbits born in a given year is equal to the number of pairs of rabbits born in each of the two previous years, starting from one pair of rabbits in the first year.
To count the number of rabbits born in the nth year, he defined the recurrence relation:
Fn = Fn-1 + Fn-2
The base cases are:
F0 = 0 and F1 = 1
Let’s write a recursive function to compute the nth Fibonacci number:
def fibonacci_recursive(n):
print("Calculating F", "(", n, ")", sep="", end=", ")
# Base case
if n == 0:
return 0
elif n == 1:
return 1
# Recursive case
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
>>> fibonacci_recursive(5)
Calculating F(5), Calculating F(4), Calculating F(3), Calculating F(2), Calculating F(1),
Calculating F(0), Calculating F(1), Calculating F(2), Calculating F(1), Calculating F(0),
Calculating F(3), Calculating F(2), Calculating F(1), Calculating F(0), Calculating F(1),
5
Naively following the recursive definition of the nth Fibonacci number was rather inefficient. As you can see from the output above, we are unnecessarily recomputing values. Let’s try to improve fibonacci_recursive by caching the results of each Fibonacci computation Fk:
from functools import lru_cache
@lru_cache(maxsize=None)
def fibonacci_recursive(n):
print("Calculating F", "(", n, ")", sep="", end=", ")
# Base case
if n == 0:
return 0
elif n == 1:
return 1
# Recursive case
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
>>> fibonacci_recursive(5)
Calculating F(5), Calculating F(4), Calculating F(3), Calculating F(2), Calculating F(1), Calculating F(0),
5
lru_cache is a decorator that caches the results. Thus, we avoid recomputation by explicitly checking for the value before trying to compute it. One thing to keep in mind about lru_cache is that since it uses a dictionary to cache results, the positional and keyword arguments (which serve as keys in that dictionary) to the function must be hashable.
Pesky Details
Python doesn’t have support for tail-call elimination. As a result, you can cause a stack overflow if you end up using more stack frames than the default call stack depth:
>>> import sys
>>> sys.getrecursionlimit()
1000
Keep this limitation in mind if you have a program that requires deep recursion.
Also, Python’s mutable data structures don’t support structural sharing, so treating them like immutable data structures is going to negatively affect your space and GC (garbage collection) efficiency because you are going to end up unnecessarily copying a lot of mutable objects. For example, I have used this pattern to decompose lists and recurse over them:
>>> input_list = [1, 2, 3]
>>> head = input_list[0]
>>> tail = input_list[1:]
>>> print("head --", head)
head -- 1
>>> print("tail --", tail)
tail -- [2, 3]
I did that to simplify things for the sake of clarity. Keep in mind that tail is being created by copying. Recursively doing that over large lists can negatively affect your space and GC efficiency.
Fin
I was once asked to explain recursion in an interview. I took a sheet of paper and wrote Please turn over on both sides. The interviewer didn’t get the joke, but now that you have read this article, hopefully you do 🙂 Happy Pythoning!
References
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Thinking Recursively in Python